Most people think drawing circles is useless. Why should you draw a circle? I don't know. It's useless. And I haven't used my implementation for any applications yet. But the implementation of drawing a circle is a good practice for the so called Slope Search ( Searching ).
Before we start the implementation of drawing a circle, we must know some properties of a circle. Most students know the equation x^2+y^2=r^2. This is the equation of a circle. The r is the radius of a circle. And I hope you understand what x and y means. They are the x and y axis.
The trick of this implementation is to hold this so-called invariant. An invariant is a condition which holds in the whole program. This condition is somethings hard to write in formula's and most of the time it need to be descripted with words. But luckily here it's easy. The invariant here is x^2+y^2=r^2.
Now we don't start at a random point (x,y) on the screen and check whether this point is true for x^2+y^2=r^2. We start at the point (0,r). So x = 0 and y = r. And if you fill in these information in the invariant you have 0^2 + r^2 = r^2. This is absolutely true. So far so good. Let's see what we've got by now:
{ precondition: must be a 'drawable' circle, so the radius must be at least 0
postcondition: a quarter circle is draw. I'll explain why we draw just a quarter circle
}
{ Invariant: x^2+y^2=r^2 }
|[var x,y:Int;
x,y:=0,r;
"place dot at (x,y)"
Do "no quarter circle is drawn"
-> "Do something with x or y"; "place dot at (x,y)";
Od
{ a quarter circle is drawn }
]|
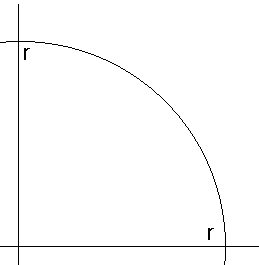
To find out what I mean with "no quarter circle is drawn" let's look to this picture

You start in the top in (0,r). What you are going to do is walking along the quarter circle until you have walked a quarter circle. That is in point (r,0). So what I mean with "no quarter circle is drawn is the condition: x >= 0. You don't have to specify y < r, because it's in the condition. The condition x >= 0 is called a guard, because it guards the condition in which a program is run.
Everything is correct now. But there's one problem. You are working with circles here. And you have to drawn a circle on a screen. Screen is devided into pixels, whole numbers, but drawing a circle you need to have real numbers, so we've got a problem. One way is to losen up the invariant a little. Let's change the invariant into x^2+y^2 <= r^2. Okay now your program look like this:
{ precondition: must be a 'drawable' circle, so the radius must be at least 0
postcondition: a quarter circle is draw. I'll explain why we draw just a quarter circle
}
{ Invariant: x^2+y^2<=r^2 }
|[var x,y:Int;
x,y:=0,r;
"place dot at (x,y)"
Do x >= 0
-> "Do something with x or y"; "place dot at (x,y)";
Od
{ a quarter circle is drawn }
]|
Now all you have to do is figure out what "Do something with x or y" means. The procedure "place dot at (x,y)" is a simple procedure that place a dot at the coordinat (x,y). You've got 2 variables, x and y. You start in (0,r) and end up in (r,0). The only thing you can do with y is decreasing it and x increasing it. But when do you increase y or decrease x? This is quite simple, because what you have to do during the whole program is to check whether the invariant holds. You're invariant is x^2 + y^2 <= r^2. If this does holds then you can easily increase x. You increase x, because you want x^2+y^2 to be near r^2 as good as possible. And if the invariant does not holds (x^2+y^2 > r^2) then you have to decrease x. After having said this. You've got the whole program for drawing a quarter circle.
{ precondition: must be a 'drawable' circle, so the radius must be at least 0
postcondition: a quarter circle is draw. I'll explain why we draw just a quarter circle
}
{ Invariant: x^2+y^2<=r^2 }
|[var x,y:Int;
x,y:=0,r;
"place dot at (x,y)"
Do x >= 0
-> if x^2+y^2 <= r^2 -> y := y - 1;
-> if x^2+y^2 > r^2 -> x := x + 1;
"place dot at (x,y)";
Od
{ a quarter circle is drawn }
]|
Now why do we draw a quarter circle? It's because a circle is very symmetric. If you have drawn a quarter circle you can copy it to the other sides. If fact you can even drawn a eighth of a circle and copy it several times an then you've got your circle. This is what I have done to. You're guard will change into x <= y. And the best of this all is that is very fast! Amazingly fast. I don't know any faster ones.
There are people who draw circles with the help of sin and cos but you know that their way isn't the easy way! This way is the easy one. And the easier the faster an implemenation is.